MATEMÁTICAS IV

 

MATEMÁTICAS lV

MATEMATICAS

INTRODUCCIÓN

En el vasto campo de las matemáticas, las relaciones y las funciones constituyen herramientas fundamentales para comprender y analizar las conexiones entre conjuntos de datos. Desde la resolución de problemas cotidianos hasta la formulación de teorías complejas, estas nociones son omnipresentes y esenciales.

Comenzando con los conceptos básicos, el dominio y el contradominio definen los conjuntos de entrada y salida de una relación o función, respectivamente. El rango y la imagen de una función revelan las posibles salidas y sus correspondientes valores en el contradominio.

La regla de correspondencia establece la asociación entre elementos del dominio y del contradominio, mientras que el discriminante y la fórmula general son herramientas útiles en el estudio de ecuaciones y relaciones algebraicas.

Dentro de las funciones, se distinguen diferentes tipos según sus propiedades. Las funciones inyectivas, o un-to-uno, asignan cada elemento del dominio a uno único en el contradominio. Por otro lado, las funciones sobreyectivas abarcan todo el contradominio, mientras que las funciones inversas invierten la relación entre los conjuntos de entrada y salida.

Además, las funciones pueden ser clasificadas como crecientes o decrecientes, dependiendo de cómo cambian sus valores a medida que aumenta el argumento. Las funciones lineales y cuadráticas son modelos comunes en el análisis matemático, y sus aplicaciones se extienden a campos tan diversos como la física, la economía y la ingeniería.

Las funciones racionales, por su parte, surgen de la relación entre dos polinomios y presentan propiedades particulares, incluyendo la existencia de asíntotas que definen el comportamiento a largo plazo de la función.

Finalmente, las funciones trascendentes, como las exponenciales y logarítmicas, amplían nuestro entendimiento más allá de los límites de la aritmética básica, permitiendo modelar fenómenos exponenciales y describir crecimientos y decaimientos en diversos contextos.

A lo largo de esta exploración, examinaremos detalladamente cada uno de estos conceptos, así como sus aplicaciones en el análisis y la resolución de problemas del mundo real.

RELACIONES Y FUNCIONES

¿Qué es una relación?

En matemáticas, una relación en un conjunto es alguna clase de vínculo que puede darse o puede no darse (sin posibilidad de estados intermedios) entre dos miembros de un conjunto determinado. Por ejemplo, "ser menor que" es una relación en el conjunto de los números naturales; que se verifica entre 1 y 3 (lo que se expresa como 1<3), y también entre 3 y 4 (denotado como 3<4); pero que no se da entre 3 y 1 ni tampoco entre 4 y 4. 

Otro ejemplo puede ayudar a clarificar el concepto: "ser hermana de" es una relación en el conjunto de todas las personas, que se cumple, por ejemplo, entre Marie Curie y Bronisława Dłuska, y viceversa.

Los miembros del conjunto no pueden estar en relación "hasta cierto punto": o están en relación, o no lo están.

video de apoyo

¿Qué es una función?

Una función matemática (también llamada simplemente función) es la relación que hay entre una magnitud y otra, cuando el valor de la primera depende de la segunda.

Por ejemplo, si decimos que el valor de la temperatura del día depende de la hora a la que la consultenos, estaremos sin saberlo estableciendo entre ambas cosas una función. Ambas magnitudes son variables, pero se distinguen entre:

Variable dependiente. Es la que depende del valor de la otra magnitud. En el caso del ejemplo, es la temperatura.

Variable independiente. Es la que define la variable dependiente. En el caso del ejemplo es la hora.

De esta manera, toda función matemática consiste en la relación entre un elemento de un grupo A y otro elemento de un grupo B, siempre que se vinculen de manera única y exclusiva. Por lo tanto, dicha función puede expresarse en términos algebraicos, empleando signos de la siguiente manera:

f: A → B

a → f(a)

En donde A representa el dominio de la función (f), el conjunto de elementos de partida, mientras que B es el codominio de la función, o sea, el conjunto de llegada. Por f(a) se denota la relación entre un objeto arbitrario perteneciente al dominio A, y el único objeto de B que le corresponde (su imagen).

Estas funciones matemáticas también pueden representarse como ecuaciones, acudiendo a variables y signos aritméticos para expresar la relación existente entre las magnitudes. Dichas ecuaciones, a su vez, podrán resolverse, despejando sus incógnitas, o bien ser graficadas geométricamente.

Puede servirte: Álgebra

Tipos de funciones matemáticas

Las funciones matemáticas pueden clasificarse de acuerdo al tipo de correspondencia que se da entre los elementos del dominio A y los de B, teniendo así lo siguiente:

Función inyectiva. Cualquier función será inyectiva si elementos distintos del dominio A se corresponden con elementos distintos del B, es decir, que ningún elemento del dominio se corresponde con la misma imagen de otro.

video de apoyo

Función sobreyectiva. Similarmente, hablaremos de una función sobreyectiva (o subyectiva) cuando a cada elemento del dominio A le corresponde una imagen en el B, incluso si ello implica compartir imágenes.

video de apoyo

Función biyectiva. Ocurre cuando una función es inyectiva y sobreyectiva a la vez, es decir, cuando a cada elemento de A le corresponde un único elemento de B, y no quedan en el codominio imágenes sin asociar, o sea, no hay elementos en B que no correspondan a uno en A.

DOMINIO:

El dominio se refiere al conjunto de todos los posibles valores de entrada (o argumentos) para los cuales una función está definida. En otras palabras, es el conjunto de valores de x para los cuales la función tiene un valor definido de y.

Por ejemplo, considera la función f(x)=1xf(x) = \frac{1}{x}f(x)=x1​. El dominio de esta función es todos los números reales excepto x=0x = 0x=0, ya que no puedes dividir entre cero en matemáticas. Entonces, el dominio de f(x)f(x)f(x) sería {x∈R∣x≠0}\{ x \in \mathbb{R} \mid x \neq 0 \}{x∈R∣x=0} o, de manera más simple, todos los números reales excepto cero.

En resumen, el dominio de una función es el conjunto de valores de entrada válidos que puedes usar en esa función.

Ejemplos de dominios en funciones comunes:

Función lineal: f(x)=2x+3f(x) = 2x + 3f(x)=2x+3

El dominio es todos los números reales, ya que no hay restricciones en los valores de xxx que puedes ingresar en una función lineal.

Función cuadrática: f(x)=x2−4f(x) = x^2 - 4f(x)=x2−4

El dominio es todos los números reales, ya que cualquier número real puede ser cuadrado y luego restarle 4.

Función raíz cuadrada: f(x)=xf(x) = \sqrt{x}f(x)=x​

El dominio son los números reales no negativos, ya que no puedes tomar la raíz cuadrada de un número negativo en el conjunto de los números reales. Entonces, el dominio sería x≥0x \geq 0x≥0.

Función racional: f(x)=1x−2f(x) = \frac{1}{x - 2}f(x)=x−21​

El dominio son todos los números reales excepto x=2x = 2x=2, ya que no puedes dividir por cero. Por lo tanto, el dominio sería x∈R∣x≠2x \in \mathbb{R} \mid x \neq 2x∈R∣x=2.

Función valor absoluto: f(x)=∣x+1∣f(x) = |x + 1|f(x)=∣x+1∣

El dominio es todos los números reales, ya que no hay restricciones en los valores de xxx que puedes ingresar en una función de valor absoluto.

Estos son solo algunos ejemplos básicos, pero el concepto de dominio se aplica a una amplia variedad de funciones matemáticas.

CONTRADOMINIO:

El contradominio es el conjunto de todos los posibles valores de salida (o imágenes) que una función podría producir. Es importante tener en cuenta que el contradominio es diferente al rango de una función.

Mientras que el dominio se refiere al conjunto de valores de entrada permitidos, el contradominio es el conjunto de todos los posibles valores de salida, independientemente de si esos valores realmente se alcanzan o no.

Por ejemplo, considera la función f(x)=x2f(x) = x^2f(x)=x2. El dominio de esta función es todos los números reales, ya que puedes cuadrar cualquier número real. El contradominio también es todos los números reales, ya que para cada valor de xxx, puedes obtener un valor de f(x)f(x)f(x) que es un número real.

Sin embargo, el rango de la función f(x)=x2f(x) = x^2f(x)=x2 es el conjunto de todos los números reales no negativos (incluyendo cero), porque los cuadrados de los números reales siempre son no negativos. Entonces, el rango de esta función sería [0,+∞)[0, +\infty)[0,+∞).

ejemplos de contradominios en funciones comunes:

Función lineal: f(x)=2x+3f(x) = 2x + 3f(x)=2x+3

El contradominio es todos los números reales, ya que cualquier número real puede ser obtenido como resultado de la función lineal al sustituir diferentes valores de xxx.

Función cuadrática: f(x)=x2−4f(x) = x^2 - 4f(x)=x2−4

El contradominio es todos los números reales, ya que cualquier número real puede ser obtenido como resultado de la función cuadrática al sustituir diferentes valores de xxx.

Función raíz cuadrada: f(x)=xf(x) = \sqrt{x}f(x)=x​

El contradominio son los números reales no negativos, ya que la raíz cuadrada de un número real no negativo siempre será un número real no negativo.

Función trigonométrica: f(x)=sin⁡(x)f(x) = \sin(x)f(x)=sin(x)

El contradominio es el intervalo [−1,1][-1, 1][−1,1], ya que el valor de sin⁡(x)\sin(x)sin(x) oscila entre −1-1−1 y 111 para cualquier valor de xxx.

Función exponencial: f(x)=exf(x) = e^xf(x)=ex

El contradominio es el conjunto de todos los números reales positivos, ya que exe^xex es siempre positivo para cualquier valor de xxx.

RANGO:

El rango se refiere al conjunto de todos los posibles valores de salida (o imágenes) que una función realmente produce. Es decir, el rango es el conjunto de valores que la función toma como resultado después de aplicar diferentes valores del dominio.

Por ejemplo, si tienes una función f(x)=x2f(x) = x^2f(x)=x2, el rango sería el conjunto de todos los números reales no negativos (incluyendo cero), ya que para cada valor de xxx, el cuadrado de xxx producirá un valor no negativo.

El rango de una función puede ser igual o más pequeño que el contradominio. Por ejemplo, la función f(x)=sin⁡(x)f(x) = \sin(x)f(x)=sin(x) tiene un contradominio de [−1,1][-1, 1][−1,1], ya que el valor de sin⁡(x)\sin(x)sin(x) oscila entre −1-1−1 y 111 para cualquier valor de xxx. Sin embargo, el rango de esta función es [−1,1][-1, 1][−1,1], ya que efectivamente toma todos los valores en ese intervalo.

El rango es una forma importante de entender el comportamiento y las propiedades de una función, ya que proporciona información sobre los posibles resultados de la función para diferentes valores de entrada.

IMAGEN DE X:

La "imagen de x" se refiere al conjunto de todos los posibles valores que pueden resultar cuando se aplica una función a un valor específico x. Formalmente, si tienes una función f, la imagen de x, denotada como f(x), es el conjunto de todos los valores y tal que y=f(x)

Por ejemplo, si tienes la función f(x)=x 2 f(x) = x2 la imagen de 3 sería 9, ya que al aplicar f a 3, obtienes 9, es decir, f(3)=9 .Sin embargo, es importante tener en cuenta que una función puede tener más de un valor de imagen para un solo valor de x, dependiendo de la función. Por ejemplo, la función f(x)=x2 tendrá como imagen de −3 tanto 9 como −9, ya que f(−3)=9y f(-3) = (-3)^2 

REGLA DE CORRESPONDENCIA:

Es un concepto fundamental en matemáticas que se refiere a la relación entre dos conjuntos, donde cada elemento del primer conjunto se relaciona de manera única con un elemento del segundo conjunto Es la forma en que se define la relación entre los elementos del dominio y los del codominio Puede expresarse mediante una fórmula matemática, una tabla de valores, una descripción verbal o cualquier otro método que especifique cómo se asignan las entradas al as salidas

POR EJEMPLO

La función tiene una regla de correspondencia que asigna cada número real x a su cuadrado x² Esto significa que si x=2, entonces f(x)=2² f(x)= x²

DISCRIMINANTE:

Sirve para resolver y hallar raíces. b²-4ac > 0 --- + Cuando es positivo obtenemos 2

raíces diferentes.

b²-4ac = 0 --- Cuando es cero obtenemos una raíz.

b²-4ac < 0 --- - Cuando es negativo no tiene raíces.

FÓRMULA GENERAL:

Es una expresión matemática formada por números e incógnitas que resolver. La resolución de la fórmula, permite obtener el valor de una incógnita en distintos casos. La fórmula general es una expresión matemática utilizada principalmente para la resolución de ecuaciones de segundo grado.

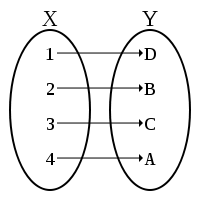
FUNCIÓN INYECTIVA

Es decir, para cualesquiera dos elementos a y b, pertenecientes al dominio de la función Domf, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura.

 En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva. Por tanto, si te piden una demostración de que una función no es inyectiva, puedes hallar dos valores distintos del dominio cuyas imágenes sean iguales. Si las encuentras, la función no es inyectiva.

INYECTIVA VS NO INYECTIVA: 

En el caso de funciones reales, para saber si son inyectivas:

Cuando están dadas mediante una ecuación, podemos utilizar la propia definición. Así, la función

f(x)=2·x+1 es inyectiva, pues: Por otro lado, la función f(x)=x2 no es inyectiva pues:

Cuando están dadas gráficamente se trata de buscar dos imágenes iguales en la misma. Observa la siguiente ilustración y lo entenderás más claramente: A la izquierda, una función real inyectiva, frente a una que no lo es, a la derecha. La prueba para determinar si una función real es inyectiva, a partir de su gráfica, consiste en buscar una recta horizontal que pueda cortar a la gráfica en más de un punto. Si la encuentras, como en el caso de la gráfica derecha, la función no es inyectiva. Si no existe ninguna recta así, como en el caso de la izquierda, la función es inyectiva. En cada gráficase han utilizado dos rectas de prueba.

FUNCIÓN SOBREYECTIVA

Una función es sobreyectiva, también llamada suprayectiva o exhaustiva, cuando el codominio y el recorrido coinciden. Formalmente: Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.

Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.

Sobreyectiva vs no sobreyectiva

A la izquierda, una función sobreyectiva. Como tal, el codominio y el recorrido coinciden. O, dicho de manera más gráfica, todos los elementos del codominio reciben flechas. A la derecha, una función no sobreyectiva. En este caso hay elementos del codominio que no están incluidos en el recorrido. Ambas funciones son no inyectivas, pues ambas cuentan con elementos en el recorrido que reciben más de una flecha. Por tanto, si te piden una demostración de que una función real es sobreyectiva, puedes hallar la imagen de dicha función. Si la imagen es el conjunto de los reales, la función es sobreyectiva. En caso contrario, no.

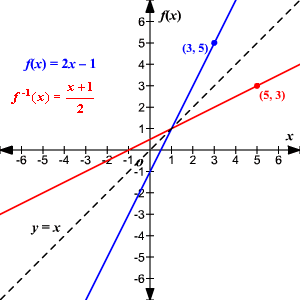
FUNCIÓN INVERSA

Una función inversa o también llamada recíproca es aquella que cumple que el dominio es igual al recorrido de la función original y su recorrido es igual al dominio de la misma función. Entonces, en lenguaje algebraico si tenemos una función; La Función inversa será;

No todas las funciones tienen una función inversa, ya que si un elemento del codominio no es imagen de un elemento del dominio, cuando se aplique su función inversa, esta no será función. Por lo tanto, para que una la función inversa exista, la función original tiene que ser biyectiva, lo que obliga que a todos los elementos de B llegue solo una flecha desde A (inyectiva y sobreyectiva a la vez), así, cuando la función inversa actúe a cada elemento de B se le asigna uno y solo uno de los elementos de A. Si f es una función que tiene por dominio al conjunto A y por rango al conjunto B , entonces se llama la función inversa de f , aquella que tiene por dominio el conjunto B y por rango al conjunto A. A la función inversa de f se le denota por Esquemáticamente esto es:

EJEMPLO:

a) Para una función g: A à B definida por el siguiente diagrama sagital;

Dada una función , su inversa es otra función, designada por de forma que se verifica que si , entonces Para encontrar la regla de correspondencia de la función inversa, se debe despejar x de la función original ya que, para la función inversa, esa es la variable dependiente.

En otras palabras se efectúa el procedimiento siguiente:

- Se define y= f(x)

- Se intercambia x por y.

- Se manipula algebraicamente para despejar y que es, es decir, la inversa de la función dada.

 

FUNCIÓN CRECIENTE

Diremos que una función es creciente cuando a medida que crece el valor de la variable independiente crece el valor de la función.

La siguiente figura muestra una función creciente, y se observa claramente que al desplazarse de izquierda a derecha sobre el eje x, el valor de la respectiva coordenada y, equivalente a f(x), va aumentando paulatinamente. Se dice que si para todo x2 > x1, entonces existe y2 > y1.

Los puntos P1 y P2 que se muestran, tienen respectivamente, coordenadas (x1, y1) y (x2,y2). Se

definen:

Δy = y2 –y1

Δx = x2 –x1

En esta función, tanto Δy como Δx tienen signo positivo, lo cual significa que y2 > y1 y x2 > x1,

respectivamente. Esta es una clara señal de que la función efectivamente crece.

Una función decreciente f es aquella cuyo valor disminuye a medida que aumenta el valor de x.

Significa que en un intervalo dado, considerando dos valores x1 y x2 tales que x1 < x2, entonces f

(x1) > f (x2)

FUNCIÓN DECRECIENTE

Diremos que una función es decreciente cuando a medida que el valor de la variable independiente aumenta el valor de la función disminuye. Al estudio de los intervalos de crecimiento y decrecimiento se le llama monotonía de la función. Asimismo, se puede considerar el crecimiento o decrecimiento de la función en un determinado punto del dominio. Pero toda función que sea decreciente en un intervalo dado, lo es también en todo punto que pertenece a él. La pendiente de la recta es m = 2 y la ordenada es n = -1 Geométricamente, cuanto mayor es la pendiente, más inclinada es la recta. Es decir, más rápido crece la función.

FUNCIÓN LINEAL

Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma

siendo m≠0.

m es la pendiente de la función

n es la ordenada (en el origen) de la función

 EJEMPLO:

Si la pendiente es positiva, la función es creciente. Si la pendiente es negativa, la función es decreciente

Ejemplo Rectas con pendientes 1, 2, 3 y -1: Puntos de corte

Una función lineal siempre corta al eje Y en un punto. También, corta al eje X en un punto.

El punto de corte con el eje Y es el punto de la recta que tiene la primera coordenada igual a 0:

El punto de corte con el eje X es el punto de la recta que tiene 0 en la segunda coordenada. Se calcula igualando a 0 la función y resolviendo la ecuación obtenida

EJEMPLO:

Calculamos los puntos de corte de la función del ejemplo anterior,

Corte con el eje Y:

Es el punto

Observad que la segunda coordenada es la ordenada.

Corte con el eje X:

Es el punto Función a partir de dos puntos Si tenemos dos puntos de la recta, podemos calcular la

expresión algebraica de la función. Sólo tenemos que sustituir las coordenadas de los puntos en la forma general de la función

APLICACIONES DE LA FUNCIÓN LINEAL

Representa la siguiente función, sabiendo que: Para poder graficar de una forma eficiente, elaboramos una tabla donde a la izquierda colocaremos los valores de x (cualquiera que nosotros queramos) y del lado derecho el valor que toma y, después de evaluar el valor asignado a x en nuestra función. La función cuadrática forma una parábola simétrica con el eje vertical.El signo del elemento que contiene el grado indica si se trata de una función convexa o cóncava

Ejemplo A

Una compañía de celulares está ofreciendo a sus clientes el siguiente plan. Puedes comprar un celular nuevo por $60 y pagar una tarifa fija mensual de $40 por mes con llamadas ilimitadas. ¿Cuánto dinero costará el plan después de 9 meses?

Solución:

 Comienza por traducir la oración a una ecuación algebraica.

cell phone=$60+$40 per month

Deja m= el número de meses y t= el costo total . La ecuación queda como: 

t(m)=60+40m

 Puedes utilizar el método de suponer y verificar o resolver esta ecuación. Sin embargo, esta sección se enfoca en la utilización de gráficos para resolver problemas. Esta ecuación es de la forma pendiente-intercepto. Cuando grafiques la recta de esta ecuación, encontrarás todos los pares ordenados que son soluciones para el problema de los teléfonos celulares.

Si encuentras el costo a los 9 meses, puedes ver que el costo es aproximadamente $425,00. Para verificar si esto es aproximadamente correcto, sustituye 9 por la variable m .PhoneCalling planTotal cost=$60=$40∗9=$360=$420.

Nuestra respuesta, $425,00 es aproximadamente igual a la solución exacta, $420,00.

FUNCIÓN CUADRÁTICA : 

Una función cuadrática es un tipo de función matemática donde la variable principal se eleva al cuadrado, es decir, se multiplica por sí misma. En términos más simples, en esta función, la variable principal aparece con un exponente 2

Propiedades de la función cuadrática

Si el signo es positivo -> la función tendrá un mínimo

en la X, y por tanto, será cóncava.

Si el signo es negativo -> la función tendrá un máximo en la X, y por tanto será convexa

Gráfico

Si le sumamos o restamos un número cualquiera, la función se desplaza arriba o abajo, en función del signo:

Si multiplicamos la función por un número cualquiera mayor a

1, la anchura de la parábola se vuelve más pequeña:

Si dividimos la función por un número cualquiera mayor a 1, la anchura de la parábola se vuelve

más grande:

video de apoyo

APLICACIONES DE LA FUNCIÓN CUADRÁTICA :

(en la vida cotidiana)

Empresas y Industrias

Ingeniería. Las funciones cuadráticas se utilizan para diseñar y analizar estructuras y sistemas

Mecánicos, como puentes y edificios. Por ejemplo, la deflexión de una viga bajo una carga se puede modelar usando una función cuadrática.

Economía. Podemos usar funciones cuadráticas para modelar la relación entre la oferta y la demanda y para analizar el equilibrio del mercado. Es decir, nos permite entender la relación entre el precio y la cantidad ofrecida y demandada en un mercado.

Geometría. Las funciones cuadráticas son usadas para definir y analizar parábolas, que son el conjunto de todos los puntos que son equidistantes de un punto fijo y una línea fija.

Vida cotidiana.

Las funciones cuadráticas resultan muy útiles en los eventos deportivos que involucran el lanzamiento de objetos como lanzamiento de jabalina o lanzamiento de disco. Por ejemplo, supongamos que lanzas un balón al aire y quieres que tu amigo lo atrape, pero quieres darle el tiempo preciso en el que el balón llegará. Podemos usar la ecuación de velocidad, la cual calcula la altura del balón basado en una ecuación parabólica o cuadrática

EJEMPLOS DE ECUACIONES CUADRÁTICAS

Ecuación cuadrática estándar: ax^2 + bx + c = 0, se utiliza para resolver problemas en los que

Se conocen los valores de a, b y c. Ecuación cuadrática en forma de vértice: a(x – h)^2 + k = 0, encontrar el vértice de una parábola y para resolver problemas en los que se conocen los valores de a, h y k.

Ecuación cuadrática en forma de factorización: (x – r1)(x – r2) = 0, encontrar las raíces de una ecuación cuadrática y para resolver problemas en los que se conocen los  valores de r1 y r2.

Ecuación cuadrática en forma de discriminante: x = (-b ± √b^2 – 4ac) / 2a, encontrar las raíces de una ecuación cuadrática y para resolver problemas en los que se conocen los valores de a, b y c.

 Ecuación cuadrática en forma de completar el cuadrado: (x + p)^2 = q, encontrar el vértice de una parábola y para resolver problemas en los que se conocen los valores de p y q.

Ejemplo A

Un cohete de juguete se lanzó al aire desde el techo de un granero. su altura (h) sobre el suelo en yardas después de (t) segundos están dados por la función. H (t) = -5t2 +10 t + 20

.a) ¿Cuál era la altura inicial del cohete?

b) ¿Cuándo alcanzó mayor altura el cohete?

Solución: Bosqueje una representación de la función. Puede utilizar una calculadora gráfica para producir el gráfico.

a)       La altura inicial del cohete es la altura desde la que se lanzó. El tiempo es cero.

 

La altura inicial del cohete de juguete es de 20 yardas. Esta es la intersección del gráfico con y.

b)      El momento en que el cohete alcanzó mayor altura es la coordenada x del vértice.

 

 El cohete de juguete necesita 1 segundo para alcanzar su altura máxima.

 FUNCIONES RACIONALES

Una función racional está definida como el cociente de polinomios en los cuales el denominador tiene un grado de por lo menos 1. En otras palabras, debe haber una variable en el denominador.

La forma general de una función racional es  , donde p ( x ) y q ( x ) son polinomios y q ( x ) ≠ 0.

Ejemplos: 

La función padre de una función racional es  y la gráfica es una hipérbola .

El dominio y rango es el conjunto de todos los números reales excepto 0.

Valor excluído  

En una función racional, un valor excluído es cualquier valor de x que hace al valor de la función y no definido. Así, estos valores deben ser excluídos del dominio de la función.

Por ejemplo, el valor excluído de la función  es –3. Esto es, cuando x = –3, el valor de y no esta definido.

Así, el dominio de esta función es el conjunto de todos los números reales excepto –3.

video de apoyo

Asíntotas

Una asíntota es una recta que se acerca a la gráfica de la función, pero nunca la toca. En la función padre  , tanto los ejes x y y son asíntotas. La gráfica de la función padre se acercará más y más pero nunca tocará las asíntotas.

Una función racional de la forma  tiene una asíntota vertical en el valor excluído, o x = b , y una asíntota horizontal en y = c .

Asíntotas horizontales

Si se satisface alguna de las siguientes dos condiciones

entonces la recta  es una asíntota horizontal para la gráfica de 

Ejemplo: Calcular las asíntotas horizontales de la función    

Calculamos el límite cuando  tiende a , para ello dividimos cada término del numerador y denominador por 

Así, la función posee una asíntota horizontal   

Asíntotas verticales

Si se satisface alguna de las siguientes dos condiciones

entonces la recta  es una asíntota vertical para la gráfica de 

Observemos que  son los puntos que no pertenecen al dominio de la función (en las funciones racionales)

Ejemplo: Calcular las asíntotas verticales de la función   

El dominio de la función es 

Calculamos los límites laterales cuando  tiende a 

Así, la función posee una asíntota vertical   

Asíntotas oblicuas

Sólo hallaremos las asíntotas oblicuas cuando no haya asíntotas horizontales.

Para que haya asíntota oblicua se tiene que cumplir que el grado del numerador sea exactamente un grado mayor que el del denominador, luego la asíntota viene dada por

donde

Ejemplo: Calcular las asíntotas de la función   

Se cumple que el grado del numerador es exactamente un grado mayor que el del denominador, solamente falta verificar si existen asíntotas horizontales.

Calculamos el límite cuando  tiende a , para ello dividimos cada término del numerador y denominador por 

Así, la función no posee asíntotas horizontales.

Para ver si posee asíntotas oblicuas, calculamos

Notemos que el dominio de la función es   y   es una asíntota vertical.

PUNTOS DE CORTE

Con eje en  x

Los "puntos de corte con el eje x" son los valores en los que una función cruza o toca el eje x en un gráfico cartesiano. Estos puntos corresponden a los valores de x para los cuales y es igual a cero. En otras palabras, son las soluciones de la ecuación y=0y = 0y=0 para la función dada.

Por ejemplo, si tienes la función y=x2−4y = x^2 - 4y=x2−4, para encontrar los puntos de corte con el eje x, necesitas resolver la ecuación x2−4=0x^2 - 4 = 0x2−4=0 para x. En este caso, los puntos de corte con el eje x serían los valores de x para los cuales la función y=x2−4y = x^2 - 4y=x2−4 toca el eje x.

Significado gráfico: Los puntos de corte con el eje x representan los puntos en los que la gráfica de una función cruza el eje x. Estos puntos son importantes para comprender el comportamiento de la función en el plano cartesiano.

Cálculo: Para encontrar los puntos de corte con el eje x para una función dada, debes resolver la ecuación y=0y = 0y=0 para la variable independiente (generalmente x). Esto implica igualar la función a cero y luego resolver la ecuación resultante para encontrar los valores de x.

Número de puntos de corte: Una función puede tener cero, uno o varios puntos de corte con el eje x. Por ejemplo, una función cuadrática puede tener dos puntos de corte con el eje x, mientras que una función lineal puede tener uno. Algunas funciones, como las funciones trigonométricas, pueden no tener puntos de corte reales con el eje x.

Importancia: Los puntos de corte con el eje x son importantes para determinar los valores de x en los que la función cruza el eje x, lo que puede proporcionar información sobre las raíces de la función (los puntos en los que la función cruza el eje y) y sobre el comportamiento de la función en diferentes regiones del plano.

Aplicaciones: En aplicaciones del mundo real, los puntos de corte con el eje x pueden tener significados importantes. Por ejemplo, en problemas de física relacionados con el movimiento de un objeto, los puntos de corte con el eje x pueden representar momentos en los que el objeto está en reposo o cambia de dirección.

Significado gráfico: Los puntos de corte con el eje x representan los puntos en los que la gráfica de una función cruza el eje x. Estos puntos son importantes para comprender el comportamiento de la función en el plano cartesiano.

Cálculo: Para encontrar los puntos de corte con el eje x para una función dada, debes resolver la ecuación y=0y = 0y=0 para la variable independiente (generalmente x). Esto implica igualar la función a cero y luego resolver la ecuación resultante para encontrar los valores de x.

Número de puntos de corte: Una función puede tener cero, uno o varios puntos de corte con el eje x. Por ejemplo, una función cuadrática puede tener dos puntos de corte con el eje x, mientras que una función lineal puede tener uno. Algunas funciones, como las funciones trigonométricas, pueden no tener puntos de corte reales con el eje x.

Importancia: Los puntos de corte con el eje x son importantes para determinar los valores de x en los que la función cruza el eje x, lo que puede proporcionar información sobre las raíces de la función (los puntos en los que la función cruza el eje y) y sobre el comportamiento de la función en diferentes regiones del plano.

Aplicaciones: En aplicaciones del mundo real, los puntos de corte con el eje x pueden tener significados importantes. Por ejemplo, en problemas de física relacionados con el movimiento de un objeto, los puntos de corte con el eje x pueden representar momentos en los que el objeto está en reposo o cambia de dirección.

video de apoyo

Ejemplo:

Hallar los puntos de corte con el eje  de la función:

Igualamos a 

Factorizamos 

De este modo

Concluimos que los puntos  y  son los puntos de corte en el eje 

Con eje en Y

Los "puntos de corte con el eje y" son los valores en los que una función cruza o toca el eje y en un gráfico cartesiano. Estos puntos corresponden al valor de y cuando x es igual a cero. En otras palabras, son las coordenadas en las que la función intersecta el eje y.

Para encontrar los puntos de corte con el eje y, debes evaluar la función cuando x es igual a cero. Por ejemplo, si tienes la función y=2x+3y = 2x + 3y=2x+3, para encontrar el punto de corte con el eje y, sustituyes x=0x = 0x=0 en la ecuación:

y=2(0)+3=3y = 2(0) + 3 = 3y=2(0)+3=3

Entonces, el punto de corte con el eje y es (0, 3), donde x es 0 y y es 3.

Los puntos de corte con el eje y son importantes porque proporcionan información sobre el valor de la función cuando x es cero, lo que a menudo es relevante para interpretar el comportamiento de la función en el gráfico.

Ejemplo:

Para hallar el punto de corte con el eje de ordenadas calculamos  haciendo .

Ejemplo

1 Hallar el punto de corte con el eje OY de la función:

Evaluamos en 

Concluimos que el punto  es el punto de corte en el eje 

Puntos auxiliares

Los puntos auxiliares en las funciones racionales son puntos adicionales que pueden ayudar a comprender mejor el comportamiento de la función y a trazar su gráfico. Las funciones racionales son aquellas en las que tanto el numerador como el denominador son polinomios.

Algunos puntos auxiliares comunes en las funciones racionales incluyen:

Puntos de corte con los ejes x e y: Como mencioné antes, los puntos de corte con los ejes x e y son útiles para entender dónde la función cruza los ejes coordenados.

Asíntotas verticales y horizontales: Las asíntotas verticales son líneas verticales que la gráfica de la función se acerca pero nunca cruza. Indican valores de x para los cuales la función se vuelve infinitamente grande o infinitamente pequeña. Las asíntotas horizontales son líneas horizontales que la gráfica de la función se acerca pero nunca cruza. Indican valores de y hacia los cuales la función tiende a medida que x se acerca a infinito o menos infinito.

Intersecciones con otras funciones: En algunos casos, puede ser útil encontrar los puntos de intersección de la función racional con otras funciones, como una función lineal, cuadrática o trigonométrica. Estos puntos pueden proporcionar información adicional sobre el comportamiento de la función racional.

Puntos críticos y puntos de inflexión: Los puntos críticos son aquellos donde la derivada de la función es igual a cero o no está definida. Los puntos de inflexión son aquellos donde la concavidad de la gráfica de la función cambia. En las funciones racionales, estos puntos pueden ser importantes para comprender la forma de la gráfica y los puntos de inflexión pueden indicar cambios en la dirección de la curvatura.

En resumen, los puntos auxiliares en las funciones racionales son aquellos que ayudan a proporcionar una imagen más completa del comportamiento de la función y su gráfica. En muchos casos, estos puntos son cruciales para entender aspectos específicos de la función, como su dominio, rango, comportamiento asintótico y puntos críticos.

video de apoyo

Gráfica

Las funciones racionales son de la forma y = f ( x ), donde f ( x ) es una expresión racional .

Algunos de los ejemplos de funciones racionales son:

Las gráficas de las funciones racionales pueden ser difíciles de dibujar. Para dibujar una gráfica de una función racional, puede comenzar encontrando las asíntotas y las intercepciones.

Pasos involucrados para graficar las funciones racionales:

Encuentre las asíntotas de la función racional, si las hay.

Dibuje las asíntotas como rectas punteadas.

Encuentre la intercepción en x y la intercepción en y de la función racional, si las hay.

Encuentre los valores de y para varios valores diferentes de x .

Grafique los puntos y dibuje una curva lisa que conecte los puntos. Asegúrese que la gráfica no cruce las asíntotas verticales.

Ejemplo:

Grafique la función racional

La asíntota vertical de una función racional es el valor de x donde el denominador de la función es cero. Iguale el denominador a cero y encuentre el valor de x .

2 x + 1 = 0

x = -1/2

La asíntota vertical de la función racional es x = -0.5.

Esta función tiene la intercepción en x en (-1/4, 0) y la intercepción en y en (0, 1). Encuentre más puntos en la función y grafique la función.

Algunas veces la función racional dada tiene que ser simplificada, antes de graficarla. En ese caso, si hay algunos valores excluidos (donde la función no esté definida) diferentes de las asíntotas, entonces hay un paso adicional involucrado al graficar la función.

Para representar la función no definida, asegúrese que la función no es una curva lisa continua en el valor excluido. Este valor excluido es usualmente referido como un hoyo en la función racional.

Por ejemplo, la función racional  tiene un hoyo en x = 0.

FUNCIONES TRANCENDENTES

Exponenciales

Las funciones exponenciales son fascinantes! Tienen la forma f(x)=axf(x) = a^xf(x)=ax, donde aaa es la base de la exponencial y xxx es el exponente, que puede ser cualquier número real.

Aquí hay algunos aspectos importantes sobre las funciones exponenciales:

Crecimiento o Decrecimiento Exponencial: El comportamiento de una función exponencial depende del valor de la base aaa:

Si 0<a<10 < a < 10<a<1, la función experimenta un decrecimiento exponencial a medida que xxx aumenta.

Si a>1a > 1a>1, la función experimenta un crecimiento exponencial a medida que xxx aumenta.

Si a=1a = 1a=1, la función es constante, ya que ax=1x=1a^x = 1^x = 1ax=1x=1 para cualquier valor de xxx.

Intersección con el Eje y: Todas las funciones exponenciales intersectan el eje y en el punto (0, 1), ya que a0=1a^0 = 1a0=1 para cualquier base aaa.

Asíntotas Horizontales: Las funciones exponenciales tienen una asíntota horizontal en y=0y = 0y=0 si 0<a<10 < a < 10<a<1 y no tienen asíntota horizontal si a>1a > 1a>1. Esto significa que la función se acerca cada vez más a cero pero nunca alcanza el eje x si 0<a<10 < a < 10<a<1.

Dominio y Rango: El dominio de una función exponencial es siempre todos los números reales. El rango depende de si la función crece o decrece exponencialmente.

Transformaciones: Las funciones exponenciales también pueden experimentar transformaciones que afectan su comportamiento, como desplazamientos verticales y horizontales, estiramiento y compresión vertical, y reflexión sobre los ejes x e y.

Aplicaciones: Las funciones exponenciales son fundamentales en diversas áreas, como la ciencia, la economía, la ingeniería y la informática. Modelan el crecimiento y la decadencia exponencial, que se encuentran en fenómenos como el crecimiento poblacional, la desintegración radioactiva, las finanzas y el procesamiento de señales.

Número de euler

El número de Euler, denotado por eee, es una constante matemática fundamental que aparece en varios contextos de las matemáticas, especialmente en el cálculo y el análisis matemático. Su valor aproximado es e≈2.71828e \approx 2.71828e≈2.71828.

El número de Euler surge naturalmente en problemas relacionados con el crecimiento y la decadencia exponencial. A menudo se define como la suma infinita de la serie:

e=∑n=0∞1n!=1+11!+12!+13!+14!+⋯e = \sum_{n=0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \cdotse=∑n=0∞​n!1​=1+1!1​+2!1​+3!1​+4!1​+⋯

Donde n!n!n! denota el factorial de nnn, que es el producto de todos los enteros positivos desde 1 hasta nnn.

El número de Euler también se puede definir como el límite de la secuencia (1+1n)n\left(1 + \frac{1}{n}\right)^n(1+n1​)n cuando nnn tiende a infinito. Es decir:

e=lim⁡n→∞(1+1n)ne = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^ne=limn→∞​(1+n1​)n

El número de Euler tiene muchas propiedades interesantes. Por ejemplo, aparece en la fórmula para el crecimiento o la decadencia exponencial continua, f(x)=exf(x) = e^xf(x)=ex, y es la base de los logaritmos naturales (logaritmos en base eee). Además, eee es irracional, lo que significa que no puede ser expresado como una fracción de dos enteros y es trascendental, lo que significa que no es raíz de ninguna ecuación algebraica con coeficientes enteros.

Función exponencial natural

La función exponencial natural se refiere a la función matemática exe^xex, donde eee es la base del logaritmo natural (aproximadamente 2.71828). Esta función es fundamental en matemáticas debido a sus propiedades únicas, especialmente en cálculo y análisis. A continuación se presentan algunas propiedades y características importantes de la función exponencial natural:

Definición: La función exponencial natural se define como:

ex=∑n=0∞xnn!e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}ex=n=0∑∞​n!xn​

donde n!n!n! (n factorial) es el producto de todos los enteros positivos desde 1 hasta nnn.

Derivada: Una de las propiedades más notables de la función exponencial es que su derivada es igual a sí misma:

ddxex=ex\frac{d}{dx} e^x = e^xdxd​ex=ex

Integral: La integral indefinida de exe^xex también es exe^xex más una constante de integración:

∫ex dx=ex+C\int e^x \, dx = e^x + C∫exdx=ex+C

Valor en cero: La función exponencial natural evaluada en cero es uno:

e0=1e^0 = 1e0=1

video de apoyo

Propiedades algebraicas:

ea+b=ea⋅ebe^{a+b} = e^a \cdot e^bea+b=ea⋅eb

e−x=1exe^{-x} = \frac{1}{e^x}e−x=ex1​

Inversa: La función inversa de exe^xex es el logaritmo natural ln⁡(x)\ln(x)ln(x), tal que:

ln⁡(ex)=xyeln⁡(x)=x\ln(e^x) = x \quad \text{y} \quad e^{\ln(x)} = xln(ex)=xyeln(x)=x

Ejemplos de uso en cálculos

Derivada de e2xe^{2x}e2x:

ddxe2x=2e2x\frac{d}{dx} e^{2x} = 2e^{2x}dxd​e2x=2e2x

Integral de e−xe^{-x}e−x:

∫e−x dx=−e−x+C\int e^{-x} \, dx = -e^{-x} + C∫e−xdx=−e−x+C

Aplicaciones

La función exponencial natural se utiliza en muchas áreas, incluyendo:

Crecimiento y decaimiento exponencial: Modela fenómenos como el crecimiento poblacional, la desintegración radiactiva y el interés compuesto.

Ecuaciones diferenciales: Muchas soluciones de ecuaciones diferenciales involucran funciones exponenciales.

Análisis complejo: En el plano complejo, exe^xex se extiende a la función eze^zez donde zzz es un número complejo.

Funciones logarítmicas

Exponente al que hay que elevar un número, llamado base, para obtener otro número determinado. Un logaritmo busca el exponente   de una base  que se ha empleado para llegar a un determinado resultado .

Ejemplo:

Si tengo de base  y como resultado , ¿a qué exponente se debe elevar el  para que nos dé como resultado ? Como te darás cuenta el valor del exponente que se utilizó para llegar al resultado  con la base  es .

La notación correspondiente para representar a un logaritmo es la siguiente:

donde  es la base,  el resultado y  el exponente buscado. Hay  que recalcar que se  deben cumplir las condiciones de que  la base sea positiva  y distinta a uno .

De la definición de logaritmo podemos decir que:

No existe el logaritmo con base negativa.

No existe el logaritmo de un número negativo.

No existe el logaritmo de cero.

El logaritmo de 1 es cero.

El logaritmo en base a de a es igual a .

El logaritmo en base a de una potencia en base a es igual al exponente.

Propiedades de los logaritmos

Propiedad del Producto: El logaritmo de un producto es igual a la suma de los logaritmos de los factores individuales.

logb​(m⋅n)=logb​(m)+logb​(n)

Propiedad del Cociente: El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.

logb​(n/m​)=logb​(m)−logb​(n)

Propiedad de la Potencia: El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base de la potencia.

logb​(mn)=n⋅logb​(m)

Propiedad del Cambio de Base: Permite convertir un logaritmo de una base a otra. Si tienes un logaritmo en base b y quieres convertirlo a base k, puedes usar la fórmula:

logb​(a)=[logk​(b)]/[logk​(a)​]

Propiedad del Logaritmo de 1: El logaritmo de 1 en cualquier base es 0, ya que cualquier número elevado a la potencia de 0 es 1.

logb​(1)=0

Propiedad del Logaritmo de la Base: El logaritmo de la base en sí mismo es siempre 1, ya que cualquier número elevado a la potencia de 1 es él mismo.

logb​(b)=1

video de apoyo

ANTOLOGIA MATEMATICAS

iiiiii